INTEGRAL

INTEGRAL

Pengertian Integral
Integral merupakan bentuk operasi matematika yang menjadi kebalikan (invers) dari operasi turunan dan limit dari jumlah atau suatu luas daerah tertentu. berdasarkan pengertian tersebut ada dua hal yang dilakukan dalam integral sehingga dikategorikan menjadi 2 jenis integral yaitu:

·                     Integral sebagai invers/kebalikan dari turunan disebut sebagai itegral tak tentu.

·                     Integral sebagai limit dari jumlah atau suatu luas daerah tertentudisebut integral tentu.

Rumus

integral f(x)dx

·                     f(x) = fungsi yang akan diintegralkan

·                     dx   = tanda untuk melakukan diferensiasi terhadap x

·                     integral f(x)dx sebagai notasi diferensiasi dari the primitive function/dari fungsi asalnya.

Rumus dasar integral:

INTEGRAL TAK TENTU
Dinamakan integral tak tentu itu karena integral ini tidak memiliki batas atas dan bawah. Biasanya hanya berupa integral dari sebuah aljabar matematika. Bentuk integral ini tidak memiliki daerah asal dan tidak memiliki daerah hasil

 ∫ f(x) dx = F(x) + c  


INTEGRAL TENTU
Dalam aplikasinya, integral tentu banyak digunakan untuk menghitung luas di bawah kurva dengan batas tertentu atau menghitung volume benda jika diputar.



INTEGRAL PARSIAL
Teknik atau metode lain yang bisa digunakan untuk melakukan integral adalah dengan metode parsial. Teknik ini biasanya digunakan untuk mencari suatu fungsi yang tidak dapat dicari integralnya jika menggunakan cara substitusi.

∫ u.dv = u.v – ∫ v. du

INTEGRAL SUBTITUSI
Untuk mengintegralkan sebuah alajabar kita bisa menggunakan metode penggantian atau substitusi. Misalkan u = g(x) dengan g(x) merupkan fungsi yang mempunyai turunan

 ∫ f(g(x)).g'(x) = ∫ f(u).du = F(u) + c

INTEGRAL FUNGSI ALJABAR
Jika ada fungsi aljabar yang diintegralkan maka sobat bisa menggunakan rumus berikut:



INTEGRAL FUNGSI EKSPONEN


INTEGRAL FUNGSI TRIGONOMETRI

Rumus:
∫ sin x dx = −cos x + C     
∫ cos x dx = sin x + C   
∫ sec2 x dx = tan x + C   
∫ csc2 x dx = −cot x + C    
∫ sec x . tan x dx = sec x + C     
∫ csc x . cot x dx = −csc x + C

Aturan-Aturan Dasar Integral 

1. Rule 1 (The Power Rule)

2. Rule 2 (The Integral Of Multiple)



3. Rule 3 (The Subtitution Rule)



4. Rule 4 (The Logarithmic Rule)



5. Rule 5 (The Exponential Rule)



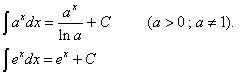
6. Rule 6 (The Integral Of Sum)



7. Rule 7 (Integration by Parts)
Jika u = u(x) dan du = u′(x) dx, sedangkan v = v(x) dan dv = v′(x) dx, lalu integration by parts dinyatakan dengan :

atau lebih jelasnya :



8. Rule 8 (Trigonometric Rules)

CONTOH SOAL